metrics

1.FAR(False Accept Rate) 误识率：人脸对比通过但实际不是本人，把假的认成真的

2.VAL(Validation Rate) 通过率：两张图是同一个人，识别出也是同一个人

3.FRR(False Reject Rate) 拒真率：1-通过率，应该是本人但是人脸对比不通过，把真的认成假的

所有metrics都建立在阈值选取的基础上，跟阈值结合起来看才有业务上的意义

通常计算一定FAR下的VAL，比如facenet千分之一FAR下的VAL为98.64%

feature extract

HOG(Histogram of Oriented Gradients)

https://www.learnopencv.com/histogram-of-oriented-gradients/

DeepLearning Loss Functions

Triplet Loss (FaceNet)

a: anchor, p: positive, n: negitive

这里的\(f(x)\)是embedding

我希望a离p更近，且有一个margin，所以，

\[||f(x_i^p) - f(x_i^a)||_2^2 + \alpha < ||f(x_i^n) - f(x_i^a)||_2^2\]

所以损失函数是，

\[L = \sum\limits_{i=1}^m max(||f(x_i^p) - f(x_i^a)||_2^2 - ||f(x_i^n) - f(x_i^a)||_2^2 + \alpha, 0)\]

Softmax Loss

将人脸识别视作多分类问题

这里的\(f(x)\)是embedding

\[L = -\frac{1}{m}\sum\limits_{i=1}^m log \frac{e^{W^T_{y_i}f(x_i) + b_{y_i}}}{\sum\limits_{j=1}^n e^{W^T_j f(x_i) + b_j}}\]

Center Loss

这里的\(f(x)\)是embedding

Softmax部分，即多分类问题的损失:

\[L = -\frac{1}{m}\sum\limits_{i=1}^m log \frac{e^{W^T_{y_i}f(x_i) + b_{y_i}}}{\sum\limits_{j=1}^n e^{W^T_j f(x_i) + b_j}}\]

Center部分，距离对应中心的距离：

\[L_C = \frac{1}{2} \sum\limits_{i=1}^m ||f(x_i) - c_{y_i}||_2^2\]

Center Loss的想法是，不仅在多分类问题上分得准，而且要更紧凑：

\[L = L_S + \lambda L_C\]

最后一个问题就是如何更新中心了：

\[c_j^{t+1} = c_j^t - \alpha \Delta c_j^t\] \[\Delta c_j = \frac{\sum\limits_{i=1}^m 1\{y_i=j\} (c_j - x_i)}{1 + \sum\limits_{i=1}^m 1\{y_i=j\}}\]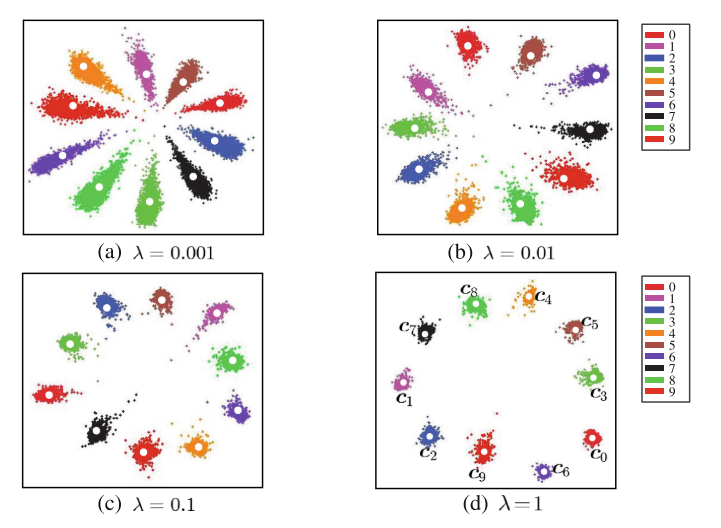

论文链接：http://ydwen.github.io/papers/WenECCV16.pdf

L-Softmax (Large-Margin Softmax)

这里的\(x\)是embedding

直观理解，当\(f(x)\)属于分类1，而不属于分类2时，Softmax想让\(W_1^Tx >W_2^Tx\)，相当于\(\|W_1\| \|x\| cos(\theta_1) > \|W_2\| \|x\| cos(\theta_2)\)

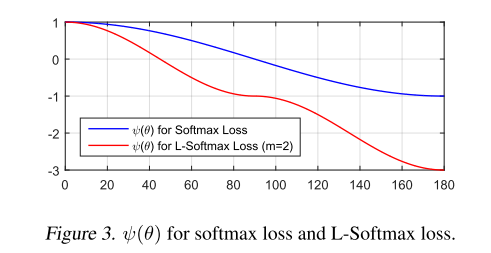
那么，L-Softmax想让这个条件更严格一些，\(\|W_1\| \|x\| cos(m\theta_1) > \|W_2\| \|x\| cos(\theta_2), 0 \leq \theta_1 \leq \frac{\pi}{m}\)，也就是原本\(\theta_1\)达到的损失，现在\(\frac{\theta_1}{m}\)时就达到了，对于\(\theta_1\)的要求更高了

L-Softmax的定义：

\[L_i = -log(\frac{e^{\|W_{y_i}\| \|x_i\| \phi(m\theta_{y_i})}}{e^{\|W_{y_i}\| \|x_i\| \phi(m\theta_{y_i})} + \sum\limits_{j \neq y_i} e^{\|W_j\| \|x_i\| cos(\theta_j)}})\]

这里的\(\phi (\theta)\)的损失为：（具体公式参考论文）

论文链接：http://proceedings.mlr.press/v48/liud16.pdf

A-Softmax (Angular Softmax, SphereFace)

这里的\(x\)是embedding

A-Softmax在L-Softmax的基础上，限定了\(\|W\|=1, b = 0\)，则\(W_1^Tx + b = \|W_1\| \|x\| cos(\theta_1) + b = \|x\| cos(\theta_1)\)，每个图片的\(x\)是相同的，所以实际上就是比较\(cos(\theta)\)。\(\|W\|\)与\(x\)角度越小，则余弦值越大，则softmax后的值越大。也就是说，与真实类别角度越小，最后的softmax出来的概率越大，分类问题跟余弦距离就契合上了（这时我们可以使用余弦距离评判人脸距离，不必使用欧几里得距离了）

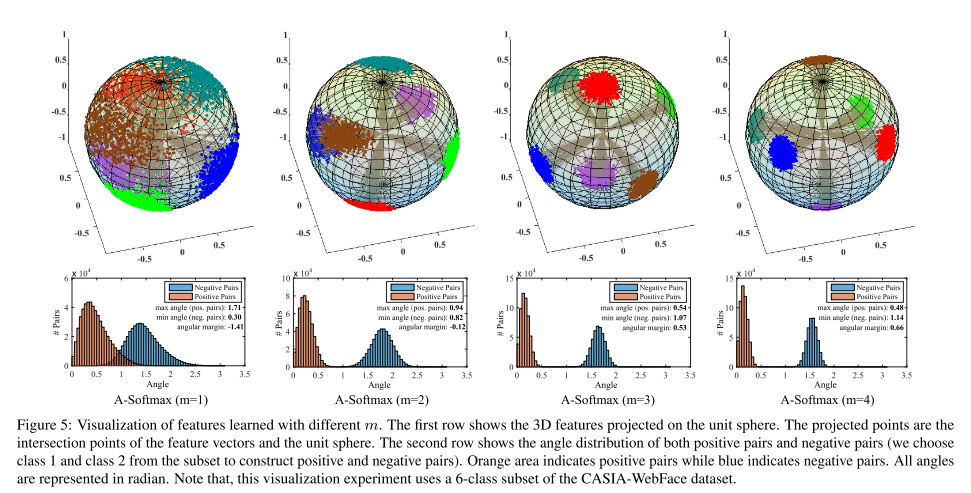
我们可以看到A-Softmax使的类间距更小了，不对\(\|W\|\)进行norm，可能会使\(\|W\|\)变大从而降低损失，而不是\(cos(\theta)\)变大而降低损失

A-Softmax的定义：

\[L_i = -log(\frac{e^{\|x_i\| \phi(m\theta_{y_i})}}{e^{\|x_i\| \phi(m\theta_{y_i})} + \sum\limits_{j \neq y_i} e^{\|x_i\| cos(\theta_j)}})\]

另外需要注意在实践中的\(m\)设置，由于\(m\)是一个非常强的限制，在\(m=2\)时，它会认为距离真实分类仍有\(2\theta\)的角度，所以比较难优化。实践中，可以使用softmax + \(\alpha\)倍的A-Softmax，刚开始\(\alpha=0\)，后面慢慢变大

论文链接：https://arxiv.org/pdf/1704.08063.pdf

NormFace

这里的\(f\)是embedding

NormFace在Softmax基础上，将embedding向量和W都标准化了，还去掉了bias，这时候softmax更加贴近余弦相似度了，文章分析了为什么会更贴近余弦相似度以及训练中可能会出现的坑

不进行norm的缺点

可以看到下图是直接使用softmax进行训练，\(f_1\)与\(f_2\)是不同类，但是距离更近，而\(f_2\)跟\(f_3\)是同类，但距离更远

另外，分类色块趋向于放射状，是由于softmax会通过增加\(f\)的大小来降低损失

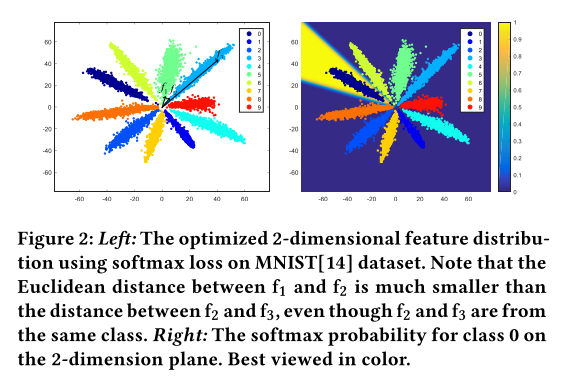
如果我们不去掉bias，即\(\|b\|>0\)，那么在原点附近就会有分类聚集

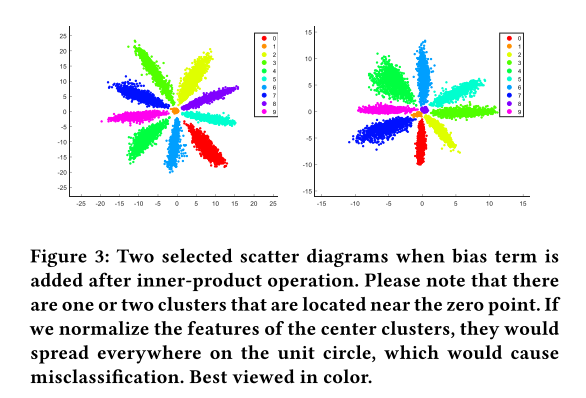
进行norm的问题：训练收敛失败

单纯的将\(f\)，\(W\)都标准化，并取消bias，会无法收敛

原因是这样做会使\(Wx\)在\([-1, 1]\)之间，也就是\(\frac{e^{W^T_{y_i}f_i}}{\sum\limits_{j=1}^n e^{W^T_j f_i}}\)无法收敛到接近1，所以需要将\(Wx\)乘以一个倍数，来让它收敛

所以NormFace的损失为： \(L_{S'} = -\frac{1}{m}\sum\limits_{i=1}^m log \frac{e^{sW^T_{y_i}f_i}}{\sum\limits_{j=1}^n e^{sW^T_j f_i}}\)

s的取值详情见论文（类数量会影响s的取值）

跟欧几里得距离的关系

由于\(\|x-y\|^2_2=2-2x^Ty\)，所以可以将损失写为，

\[L_{S'} = -\frac{1}{m}\sum\limits_{i=1}^m log \frac{e^{sW^T_{y_i}f}}{\sum\limits_{j=1}^n e^{sW^T_j f}} = -\frac{1}{m}\sum\limits_{i=1}^m log \frac{e^{-\frac{s}{2}\|f_i - W_{y_i}\|_2^2}}{\sum\limits_{j=1}^n e^{-\frac{s}{2}\|f_i - W_j\|_2^2}}\]

所以这个时间余弦相似度跟欧几里得距离实质是一样的

我们可以将\(\|f_i - W_j\|_2^2\)带入到contrastive loss或者triplet loss中，这样就解决了这两种loss是使用欧几里得距离的问题了（不过要注意margin的设置，具体可见论文）

论文链接：https://arxiv.org/pdf/1704.06369.pdf

AM-Softmax (Additive Margin Softmax)

CosFace也是一样的思路

这里的\(f\)是embedding

AM-Softmax将\(f\)，\(W\)都标准化，并取消bias。特别的，它使用的margin方式是\(\phi(\theta) = cos(\theta) - m\)

所以最终的损失是： \(\begin{aligned} & l_{AMS} = -log(\frac{e^{s\cdot (cos(\theta_{y_i}) - m)}}{e^{s\cdot (cos(\theta_{y_i}) - m)} + \sum\limits_{j \neq y_i} e^{s\cdot cos(\theta_j)}}) \\ & \qquad = -log(\frac{e^{s\cdot (W_{y_i}^T f - m)}}{e^{s\cdot (W_{y_i}^T f - m)} + \sum\limits_{j \neq y_i} e^{s\cdot W_{j}^T f}}) \\ \end{aligned}\)

论文链接：https://arxiv.org/pdf/1801.05599.pdf

ArcFace

这里的\(f\)是embedding

ArcFace将\(f\)，\(W\)都标准化，并取消bias。它使用的margin方式是\(\phi(\theta) = cos(\theta - m)\)

所以最终的损失是：

\[l = -log(\frac{e^{s\cdot (cos(\theta_{y_i} + m))}}{e^{s\cdot (cos(\theta_{y_i} + m))} + \sum\limits_{j \neq y_i} e^{s\cdot cos(\theta_j)}})\]

我们可以将A-Softmax、AM-Softmax（CosFace）、ArcFace结合在一起：

\[l = -log(\frac{e^{s\cdot (cos(m_1\theta_{y_i} + m_2) - m_3)}}{e^{s\cdot (cos(m_1\theta_{y_i} + m_2) - m_3)} + \sum\limits_{j \neq y_i} e^{s\cdot cos(\theta_j)}})\]

这里对比一下三者在几何学上的差别

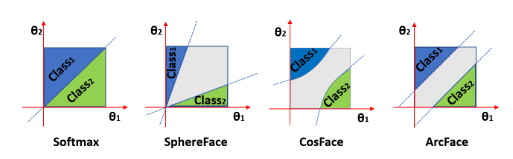
论文链接：https://arxiv.org/pdf/1801.07698.pdf