Gradient Descent

Batch gradient descent

每次迭代对所有的样本计算梯度，然后进行梯度下降，公式为：

\[\theta = \theta - \eta\nabla_\theta J(\theta)\]

优点：对于凸损失可以优化到全局最优，对于非凸的会优化到一个局部最优

缺点：样本量级变大后太慢

Stochastic gradient descent

每次迭代仅使用一个样本进行梯度下降，公式为：

\[\theta = \theta - \eta\nabla_\theta J\left(\theta;x^{(i)};y^{(i)}\right)\]

随机梯度下降解决了批梯度下降每次迭代使用太多样本的问题，但是由于每次只用一个样本，会让损失下降时震荡的很厉害

Mini-batch gradient descent

每次迭代使用一些样本进行梯度下降（比如64个样本），公式为：

\[\theta = \theta - \eta\nabla_\theta J\left(\theta;x^{(i:i+n)};y^{(i+n)}\right)\]

但是minibatch梯度下降在复杂模型中非常难调参，比如在神经网络，或者在FM中，要花很多时间调参才能让模型收敛，困难有下面几个方面：

学习率、是否衰减、如何衰减等超参难以选择（有时候调参的代价也很大，跑一次很久）
不同的参数可能需要不同的学习率
很多复杂模型非凸，下降到局部最优可能还是可以接受的，但是更多的情况是收敛到鞍点（saddle points），这是无法接受的

Momentum

当损失函数的样子很像狭长的山谷时，SGD会在山谷之间震荡，如下图左边所示：

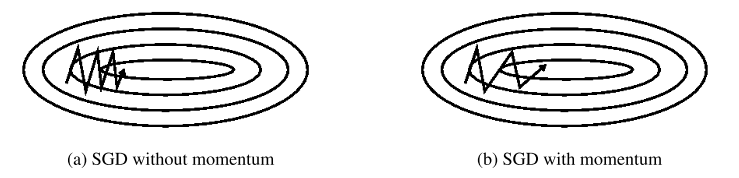
而momentum方法会缓解这个问题，我们先看一下公式：

\[\begin{align} &v_t = \gamma v_{t-1} + \eta\nabla_\theta J(\theta) \\ &\theta = \theta - v_t \\ \end{align}\]

通常\(\gamma = 0.9\)

如果某个维度一直在下降，比如图中的水平方向，那么momentum会进行加速，因为\(v_t\)和\(v_{t-1}\)方向一致；如果某个维度一直在震荡，比如图中的垂直方向，那么momentum会进行抑制，因为\(v_t\)和\(v_{t-1}\)方向相反。所以momentum会很好的缓解上面提到SGD的缺点

另外，我们可以把momentum想象成一个球放到山谷里，这个球是有惯性的，由于惯性它会不断加速

测试效果如下（代码在github）：

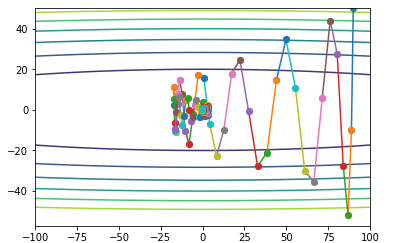
NAG(Nesterov accelerated gradient)

从上面momentum的效果可以看出，因为惯性的原因，球会跑过头，NAG就是为了解决这个问题。NAG想要得到一个更聪明的球，当再次上坡时减速。NAG的公式：

\[\begin{align} &v_t = \gamma v_{t-1} + \eta\nabla_\theta J(\theta - \gamma v_{t-1}) \\ &\theta = \theta - v_t \\ \end{align}\]

NAG可以理解为提前预估参数的下个位置大概在哪里，预估的下一个位置就是\(\theta - \gamma v_{t-1}\)，momentum用了当前位置的梯度，而NAG用了下一个位置的梯度。也就是如果球在“跑过头”的状态，NAG预估下一个位置，如果“跑过头”那么下个位置的梯度绝对值会更大一些，那么就会更多的抑制惯性，从而让球提前减速，可以观察下面实验的结果，垂直方向“跑过头”的现象就没了（其实正常应该是缓解，下面数据刚好得到没有跑过头的结果）。另外，水平方向上的加速会被削弱，因为水平方向下一个位置的梯度绝对值更小，所以加速也被NAG抑制了。跟momentum对比，momentum用了当前位置的梯度，而NAG用了下一个位置的梯度，那NAG相当于在momentum基础上多了下一个位置梯度和当前位置梯度的差值（有点二阶导的意思？）。

测试效果如下：

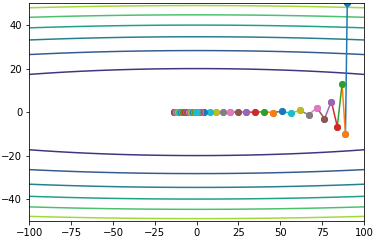
Adagrad

Adagrad会让每个维度的更新处在同一个尺度，梯度绝对值小的更新幅度小，梯度绝对值大的更新幅度大。对于稀疏数据，不频繁出现的参数会更新幅度变大，频繁出现的参数更新幅度变小。公式为：

\[\begin{align} &G_t = G_t + g_t^2 \\ &\theta = \theta - \frac{\eta}{\sqrt{G_t + \epsilon}} \circ g_t \\ \end{align}\]

测试效果如下：

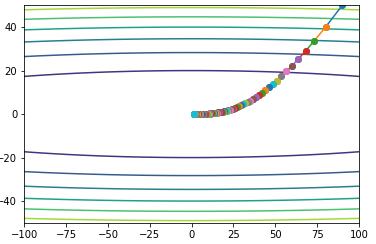
将学习率放大10倍，前期震荡，后面也是能收敛：

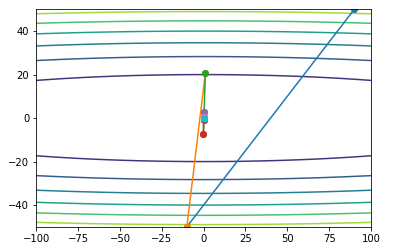
Adadelta

Adagrad是保留所有梯度的平方和，这样会使分母单调变大（也就是学习率会一直衰减），而Adadelta使用了指数移动平均：

\[E\left[ g^2 \right]_t = \gamma E\left[ g^2 \right]_{t-1} + (1-\gamma)g_t^2\]

所以，参数的变化为：

\[\Delta\theta_t = - \frac{\eta}{\sqrt{E\left[ g^2 \right]_t + \epsilon}} \circ g_t\]

分母就是root mean squared（RMS），所以直接将分母换掉：

\[\Delta\theta_t = - \frac{\eta}{RMS\left[ g \right]_t} \circ g_t\]

然后Adadelta为了解决单元不匹配的问题（这个细节等看了原文再补充），做了以下改进

\[\begin{align} &E\left[\Delta\theta^2\right]_t = \gamma E\left[\Delta\theta^2\right]_{t-1} + (1-\gamma)\Delta\theta^2_t \\ &RMS\left[\Delta\theta\right]_t = \sqrt{E\left[\Delta\theta^2\right]_t + \epsilon} \\ \end{align}\]

然后替换学习率，这样就消除了学习率，不需要调这个超参了。由于在\(t\)的时候不知道\(RMS\left[\Delta\theta\right]_t\)，所以使用\(RMS\left[\Delta\theta\right]_{t-1}\)，最终公式为：

\[\begin{align} &\Delta\theta_t = -\frac{RMS\left[\Delta\theta\right]_{t-1}}{RMS\left[g\right]_t} g_t \\ &\theta_{t+1} = \theta_t + \Delta\theta_t \\ \end{align}\]

测试效果如下：

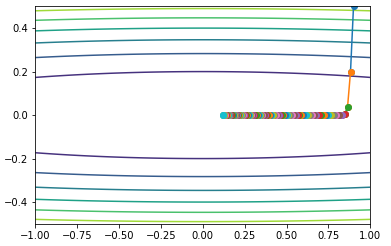
虽然理论上Adadelta不需要调学习率，但收敛情况受\(\epsilon\)的影响很大，所以个人感觉相当于从调学习率变成了调\(\epsilon\)

RMSprop

RMSprop跟Adadelta几乎同时被提出，RMSprop也是解决Adagrad学习率衰减的问题，公式为：

\[\begin{align} E\left[ g^2 \right]_t &= \gamma E\left[ g^2 \right]_{t-1} + (1-\gamma)g_t^2 \\ \theta_{t+1}& = \theta_{t} - \frac{\eta}{\sqrt{E\left[ g^2 \right]_t + \epsilon}} g_t \\ \end{align}\]

RMSprop跟没替换学习率之前的公式实际是一致的

\(\gamma\)通常为0.9，\(\eta\)通常为0.001

测试效果如下：

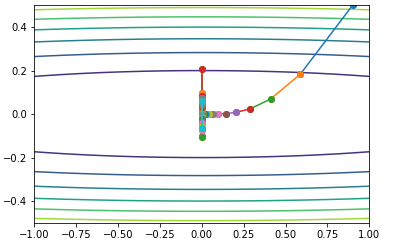
Adam(Adaptive Moment Estimation)

Adam结合了momentum和RMSprop的特性，每次先计算：

\[\begin{align} m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\ v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ \end{align}\]

然后，因为\(m_t\)和\(v_t\)在初始的时候是0，所以在最初的几轮值会偏小，所以需要\(\beta_1\)和\(\beta_2\)对其进行修正，修正的公式为：

\[\begin{align} \hat{m}_t &= \frac{m_t}{1-\beta_1^t} \\ \hat{v}_t &= \frac{v_t}{1-\beta_2^t} \\ \end{align}\]

最初的几轮，分母会比1小，这样就会把分子调大（即进行了修正）。到后面，分母接近于1，这时分子的值几乎不会变了，也就是到会面不进行修正

最终梯度更新的公式为：

\[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t}+\epsilon} \hat{m}_t\]

通常\(\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8}\)

测试效果如下：

我这里特意调大了学习率，所以曲线看起来很妖，我们从中可以看到ada系列的梯度下降，会让每个维度尺度一致，也就是方向会往中间（而不用ada的时候像上面momentum的图一样，会跟随数值大的维度的梯度走）；momentum系列会让梯度在震荡时候趋于稳定（震荡越来越小）