forward/backward propagation
-
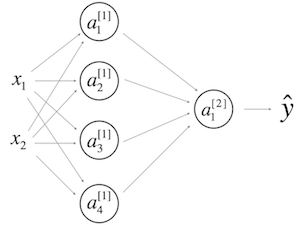
notation
\(n^{[i]}\): 代表第i层的节点数,i=0代表输入特征数
\(m\): 代表训练的样本数
\(W^{[i]}\): 代表第i-1层到第i层的权值,大小为\((n^{[i]}, n^{[i-1]})\)
\(b^{[i]}\): 代表第i-1层到第i层的偏置,大小为\((n^{[i]}, 1)\)
\(Z^{[i]}\): 代表第i层的值,大小为\((n^{[i]}, m)\)
\(A^{[i]}\): 代表第i层节点通过激活函数后的值,大小为\((n^{[i]}, m)\),特别的\(A^{[0]}=X\)
\(g^{[i]}\): 代表第i层的激活函数
-
forward propagate
- back propagate
W初始化问题
-
有隐藏层
W不能都初始化为0,因为这样会使\(A^{[1]} = 0\),继而使\(\frac{\partial{J}}{\partial{W^{[2]}}} = \frac{\partial{J}}{\partial{Z^{[2]}}} \cdot A^{[1]T} \cdot \frac{1}{m} = 0\),则\(W^{[2]}\)不会变,\(W^{[1]}\)同样,无论进行几次迭代都一样
-
无隐藏层
W可以初始化为0,因为即使W为0,\(\frac{\partial{J}}{\partial{W^{[1]}}} = \frac{\partial{J}}{\partial{Z^{[1]}}} \cdot A^{[0]T} \cdot \frac{1}{m}\)也不会为0,它直接取决于\(X\)
-
梯度消失/爆炸
在很深的网络中,很容易造成梯度消失或者梯度爆炸,合理的初始化W,能使这种情况减缓。
直观感受(不严谨的),每层得到的值都比1大一些,比如1.5,到最后这个值就会爆炸;每层得到的值都比1小一些,比如0.5,到最后这个值就会消失。所以尽量让每层的值更靠近1,那么让z=w1x1+w2x2+…+xnxn尽量为1的方法,可以让wi=1/n
-
推荐的初始化
初始化为一个比较小的值(太大会导致学习很慢)
\[W^{[l]} = np.random.rand(shape) * np.sqrt(\frac{1}{n^{[n-1]}})\]如果激活函数是relu,一般后面的项为\(np.sqrt(\frac{2}{n^{[n-1]}})\)
如果激活函数是tanh,一般后面的项为\(np.sqrt(\frac{1}{n^{[n-1]}})\)
还有其他的选择,如\(np.sqrt(\frac{2}{n^{[n-1]}+n^{[n]}})\)在实际运用中可以作为超参,比较哪种初始化好
梯度下降优化
momentum
直观解释,球会受到前面下降的影响,有一些惯性;另外,如果某个方向波动的厉害,那么momentum能很好的处理这种情况,
初始化,\(v_{dW}=0\),\(t\)为第几个周期
每次迭代,
\[\begin{align} &v_{dW}=\beta_1 v_{dW} + (1-\beta_1) dW \\ &v_{dW}^{corrected}=\frac{1}{1-\beta_1^t} v_{dW}(偏差修正,一般在momentum不作修正) \\ &W = W - \alpha \cdot v_{dW} \\ \end{align}\]关于偏差修正:在刚开始迭代的时候,v为0,接下来几次v都会非常小,偏差修正是为了纠正这个误差
RMSprop
直观解释,不同方向梯度尺度不同,而学习率是同一个,所以球位移很大的方向,需要给予抑制
初始化,\(s_{dW}=0\)
每次迭代,
\[\begin{align} &s_{dW}=\beta_2 s_{dW} + (1-\beta_2) dW^2 \\ &s_{dW}^{corrected}=\frac{1}{1-\beta_2^t} s_{dW}(偏差修正,一般不用) \\ &W = W - \alpha . \frac{dW}{\sqrt{s_{dW}} + \epsilon}\\ \end{align}\]Adam
直观解释,momentum和RMSprop的结合
初始化,\(v_{dW}=0\),\(s_{dW}=0\)
每次迭代,
\[\begin{align} &v_{dW}=\beta_1 v_{dW} + (1-\beta_1) dW \\ &v_{dW}^{corrected}=\frac{1}{1-\beta_1^t} v_{dW} \\ &s_{dW}=\beta_2 s_{dW} + (1-\beta_2) dW^2 \\ &s_{dW}^{corrected}=\frac{1}{1-\beta_2^t} s_{dW} \\ &W = W - \alpha . \frac{v_{dW}^{corrected}}{\sqrt{s_{dW}^{corrected}} + \epsilon} \\ \end{align}\]Overfitting
过拟合原因:数据太少 or 模型太复杂
DropOut
L1 / L2
early stopping
add datasets
- data argumentation
Batch Normalization
每层的\(Z^{[l]}\)都进行归一化后得到\(\tilde{Z}^{[l]}\)后再计算\(A^{[l]}\)
-
使每层在训练的时候更稳定,由于每层都做过归一化,即使训练数据变化比较大,归一化后它的分布也不会变化很大,大概意思就是减少了层与层直接的耦合
-
具有轻微的正则化效果(不过这个不重要,正则化不是BN的目的)
公式:
\[\begin{align} &\mu = \frac{1}{m} \sum\limits_{i} z^{(i)} \\ &\sigma^{2} = \frac{1}{m} \sum\limits_{i}(z^{(i)}-\mu)^2 \\ &z^{(i)}_{norm} = \frac{z^{(i)}-\mu}{\sqrt{\sigma^2 + \epsilon}} \\ &\tilde{z}^{(i)} = \gamma z^{(i)}_{norm} + \beta \\ \end{align}\]其中,\(\gamma\)和\(\beta\)也在梯度下降的时候进行更新(像W和b一样)
经典的CNN
-
LeNet (1986)
首次使用卷积、池化、全连接层得到很好的效果,在此之后CNN沉寂了十几年
-
AlexNet (2012)
更复杂的CNN,使用了GPU,让CNN和GPU火了起来
-
GoogLeNet (2014)
多个卷积结果concat
1×1 CONV
由Inception块,每个块后面都有输出 -
VGG (2014)
更深的卷积、池化、全连接层。。计算量巨大(结构其实不复杂)
-
ResNet (2016)
Res block(高宽不变)和Conv block(高宽变小),使得CNN能够更深,不易出现梯度消失/爆炸
Res block更容易学习为Identity function
目标探测(object detection)
Sliding Windows
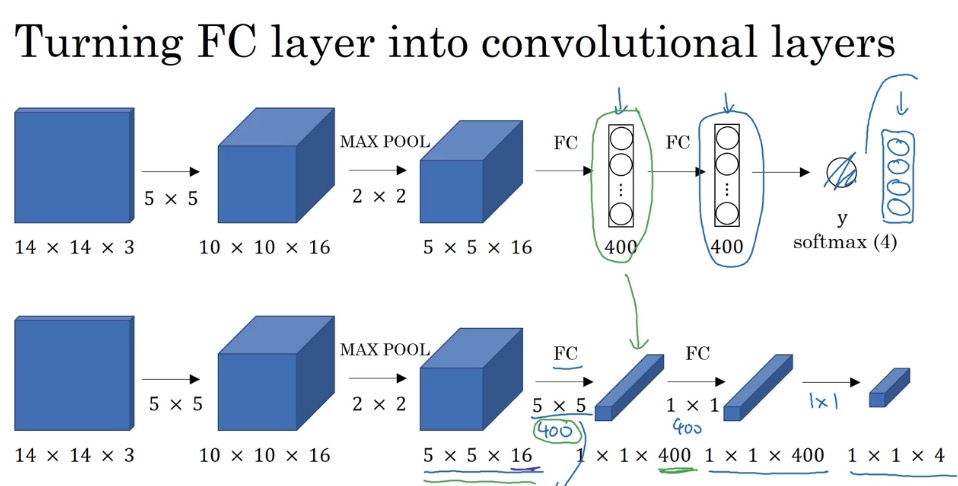
首先将FC层转换成卷积层,这个转换实际上是等效的,因为下面的filter是5×5×16的,实际上就是线性相乘,然后得到一个值,400个filters就是400个值
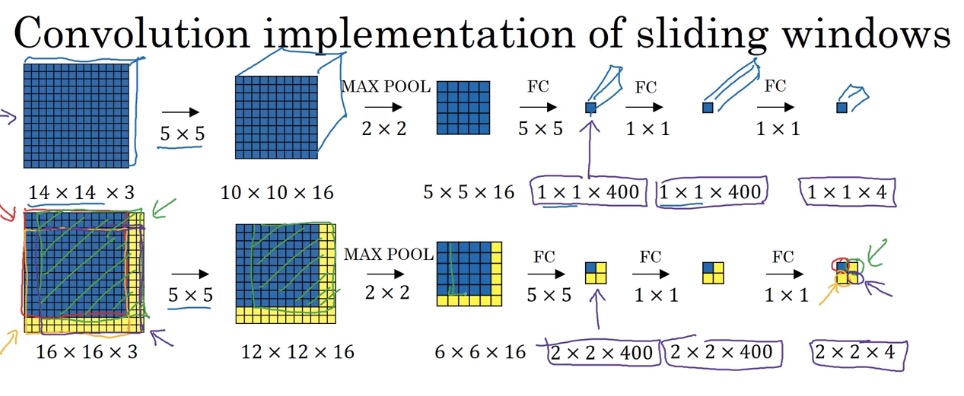
接下来直接将原图放到网络中,这样可以同时对四个块进行计算,节省的公共部分的计算 而每个块都是共用所有的卷积核的
YOLO(Your Only Look Once)
将图片分成3×3的块进行探测,但注意,不是分别进行预测,而是同时预测
假设输出的\(y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3]\),
其中,分别代表:框内是否有物体,中心x,中心y,物体高,物体宽,是否为行人,是否为车,是否为摩托车
那么,一张子图片最终输出的shape为1×1×8,
分成3×3后的输出为3×3×8,然后一起训练/预测

IoU(Intersection over Union)
计算两个框重合度的方法 \(IoU=\frac{A \cap B}{A \cup B}\)
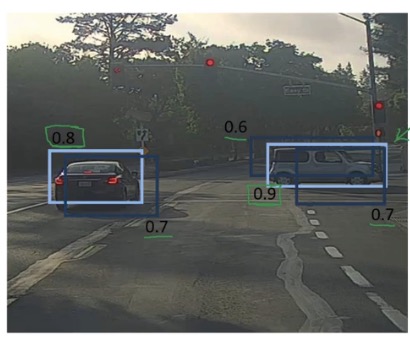
Non-max suppression
对一个图预测后,会得到很多框,该如何去确定哪些框要留下
1.首先去掉\(P_c\)太低的,也就是有物体概率低的框
2.选取剩下框中,概率最高的,代表这个框有物体,然后去掉跟这个框重合度高的;这个步骤循环进行
Faster Alogrithms
Propose regions是指大致找出物体所在位置
R-CNN: Propose regions(traditional segmentation algorithms). Classify proposed regions one at a time. Output label + bounding box. 候选框 + 缩放 + CNN提取特征 + SVM
Fast R-CNN: Propose regions. User convolution implementation of sliding windows to classify all the proposed regions. 候选框 + ROI pooling + CNN
Faster R-CNN: Use convolutional network to propose regions. 整图进CNN+PRN(Region Proposal Networks,archorBox + softmax)+ softmax
Nerual Style Transfer
cost function
C代表content图片,S代表style图片,G代表generate图片
- content cost function
评判内容是否接近的标准是某一层C和G的激活值是否接近
\[J_{content}(C,G) = \frac{1}{4 \times n_H \times n_W \times n_C}\sum _{ \text{all entries}} (a^{(C)} - a^{(G)})^2\]- style cost function
这里使用gram matrix来衡量style,具体的,它代表了每个filter之间相关程度,对角线呈现了每个filter自身的一个评判(大概是这个意思,并没有一个推导,不过实际应用起来效果不错)
\[\begin{aligned} &{\displaystyle G_{ij} = v_{i}^T v_{j} = np.dot(v_{i}, v_{j}) } \\ &J_{style}^{[l]}(S,G) = \frac{1}{4 \times {n_C}^2 \times (n_H \times n_W)^2} \sum _{i=1}^{n_C}\sum_{j=1}^{n_C}(G^{(S)}_{ij} - G^{(G)}_{ij})^2 \\ &J_{style}(S,G) = \sum_{l} \lambda^{[l]} J^{[l]}_{style}(S,G) \\ \end{aligned}\]- total cost function
实际应用中,\(J(C,G)\)使用某一层来做,\(J(S,G)\)使用多层去做,效果更好
GRU(Gated Recurrent Unit)
architecture
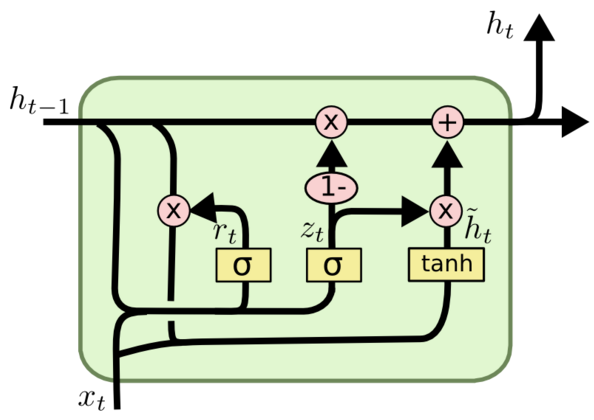
\(r_t\)代表重置门,\(z_t\)代表更新门
\[\begin{aligned} &r_t = \sigma (W_r [h_{t-1},x_t] + b_r) \\ &z_t = \sigma (W_z [h_{t-1},x_t] + b_z) \\ &new memory: \tilde{h_t} = tanh(W_h [r_t * h_{t-1},x_t] + b_h) \\ &hidden state: h_t = z_t * \tilde{h_t} + (1-z_t) * h_{t-1} \\ \end{aligned}\]直观上讲一下更新门\(z_t\),如果它接近于0,则保留\(\tilde{h_t}\),\(\tilde{h_t}\)可以理解为memory;如果它接近于1,则保留\(h_{t-1}\),即上一个hidden state
LSTM(Long Short Term Memory)
architecture

遗忘门\(f_t = \sigma (W_f [h_{t-1},x_t] + b_f)\)
输入门\(i_t = \sigma (W_i [h_{t-1},x_t] + b_i)\)
new memory \(\tilde{C_t} = tanh(W_C [h_{t-1},x_t]) + b_C)\)
记忆单元\(C_t = f_t * C_{t-1} + i_t * \tilde{C_t}\)
输出门\(o_t = \sigma (W_o [h_{t-1},x_t] + b_o)\)
输出(hidden state)\(h_t = o_t * tanh(C_t)\)
text translate(Seq2Seq)
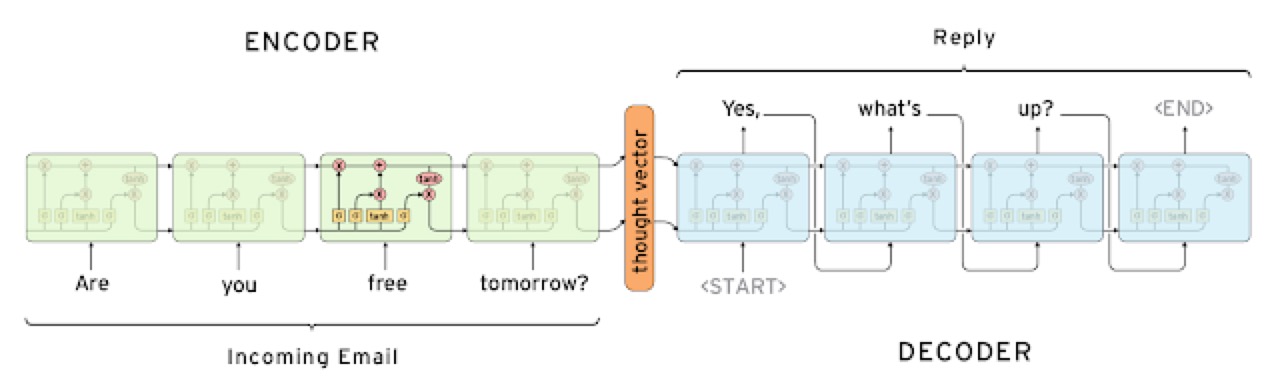
前面一半是encode过程,后面一半是decode过程,先将要翻译的文本通过encode块,再通过decode块生成目标语言
Beam Search
假设beam_width B=3,
在生成第一个单词时,保留3个可能性最高的单词 在生成第二个单词时,计算出上面得到的3个单词乘上第二个单词的概率,得到单词对(单词1, 单词2)的备选概率,选最高的3个 重复上述操作
Attention Model
大致思路就是在生成一个单词时,不仅注意前一个单词,也注意X每个单词
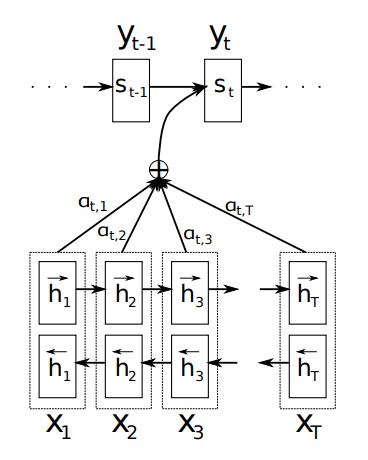
Speech Recognition
CTC (Connectionist Temporal Classification)
将RNN预测出的语音(讲的内容,会很长,好几个时间单位都在一个字母上),转化成正常单词
__c_oo_o_kk___b_ooooo__oo__kkk
->
cookbook