拉格朗日对偶性
- 原始问题
引进拉格朗日函数, \(L(x, \alpha, \beta)=f(x) + \sum\limits^k_{i=1}\alpha_i c_i(x) + \sum\limits^l_{j=1}\beta_j h_j(x)\) 这里,\(\alpha_i \ge 0\)
考虑函数, \(\theta_P(x) = \max\limits_{\alpha , \beta} L(x, \alpha, \beta)\) 这里\(P\)代表原始问题
求解原问题,即求解 \(\min\limits_{x} \theta_P(x) = \min\limits_{x} \max\limits_{\alpha , \beta} L(x, \alpha, \beta)\)
定义原始问题的最优解 \(p^* = \min\limits_{x} \theta_P(x)\)
- 对偶问题
\(\theta_D(\alpha, \beta) = \min\limits_{\alpha, \beta}L(x, \alpha, \beta)\) 这里\(D\)代表对偶问题
对偶问题的最优解, \(d^* = \theta_D(\alpha, \beta)\)
- 原始问题和对偶问题的关系
- KKT条件
满足KKT条件时,\(d^* = p^*\)
线性可分支持向量机(硬间隔最大化)
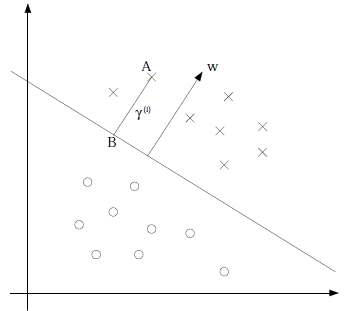
下图中的三个点,A距离分类边界很远,我们可以很确定A是X类;而C距离分类边界很近了,它属于X类的确信度就不是很高了;而B在AC之间,确信度也在AC之间。所以我们想让离分类边界最近的点,尽可能离分类边界远

我们定义函数间隔: \(\hat\gamma_i = |wx_i+b| = y_i(wx_i+b)\)
几何间隔: \(\gamma_i = \frac{|wx_i+b|}{\lVert w \rVert} = \frac{y_i(wx_i+b)}{\lVert w \rVert}\)
它们之间的关系是: \(\gamma_i = \frac{\hat\gamma_i}{\lVert w \rVert}\)
我们先假设数据线性可分,基于上面的想法,我们想让离分类边界(几何间隔)最近的点,尽可能离分类边界远,也就是使,
\[\begin{aligned} &\max \quad \gamma \\ &s.t. \quad \frac{y_i(wx_i+b)}{\lVert w \rVert} \ge \gamma \end{aligned}\]转化成函数间隔后,
\[\begin{aligned} &\max \quad \frac{\hat\gamma}{\lVert w \rVert} \\ &s.t. \quad y_i(wx_i+b) \ge \hat\gamma \end{aligned}\]由于我们求\(\frac{\hat\gamma}{\lVert w \rVert}\)最大时,\(\hat\gamma\)的取值不会影响这个最优化问题,所以我们取\(\hat\gamma=1\),则最优化问题变成了,
\[\begin{aligned} &\min \quad \frac{1}{2}\lVert w \rVert^2 \\ &s.t. \quad y_i(wx_i+b) \ge 1 \end{aligned}\]根据这个最优化问题,我们列出拉格朗日函数,
\[L(w,b,\alpha) = \frac{1}{2}\lVert w \rVert^2 + \sum\limits^N_{i=1}\alpha_i [y_i(wx_i+b)-1]\]那么,原问题就是,
\[p^* = \min\limits_{w,b} \max\limits_{\alpha} L(w,b,\alpha)\]它的对偶问题是,
\[d^* = \max\limits_{\alpha} \min\limits_{w,b} L(w,b,\alpha)\]由于优化问题满足KKT条件,所以可以直接求解对偶问题 那么我们先求\(\min\limits_{w,b} L(w,b,\alpha)\)
\[\frac{\partial L(w,b,\alpha)}{\partial w} = w - \sum\limits^N_{i=1}\alpha_i y_i x_i = 0 \\ \frac{\partial L(w,b,\alpha)}{\partial b} = - \sum\limits^N_{i=1}\alpha_i y_i = 0 \\\]得到,
\[w = \sum\limits^N_{i=1}\alpha_i y_i x_i \\ \sum\limits^N_{i=1}\alpha_i y_i = 0 \\\]代入\(L(w,b,\alpha)\)中,得到
\[L(w,b,\alpha) = \sum\limits^N_{i=1}\alpha_i - \frac{1}{2} \sum\limits^N_{i=1} \sum\limits^N_{j=1} \alpha_i \alpha_j y_i y_j x_i x_j\]然后再进行极大化过程,
\[\begin {aligned} &\max \quad \sum\limits^N_{i=1}\alpha_i - \frac{1}{2} \sum\limits^N_{i=1} \sum\limits^N_{j=1} \alpha_i \alpha_j y_i y_j x_i x_j \\ &s.t. \quad \sum\limits^N_{i=1}\alpha_i y_i = 0 \\ &\qquad \quad \alpha_i \ge 0, i=1,2,...,N \end{aligned}\]根据上式可以求得\(a^*\),则可以进一步求得\(w^*,b^*\)
最终决策函数为,
\[f(x) = sign(\sum\limits^N_{i=1} \alpha_i^* y_i (x\bullet x_i)+b^*)\]线性支持向量机(软间隔最大化)
对于实践中的数据,很多时候都是线性不可分的,所以这时候我们引入一个松弛因子\(\xi\),则点的约束条件变成了,
\[\hat\gamma_i = y_i(wx_i+b) \ge 1-\xi_i\]这时候优化问题变成了,
\[\begin {aligned} &\min \quad \frac{1}{2}\lVert w \rVert^2 + C\sum\limits^N_{i=1}\xi_i \\ &s.t. \quad y_i(wx_i+b) \ge 1 \end{aligned}\]求解后得到,
\[\begin {aligned} &\max \quad \sum\limits^N_{i=1}\alpha_i - \frac{1}{2} \sum\limits^N_{i=1} \sum\limits^N_{j=1} \alpha_i \alpha_j y_i y_j x_i x_j \\ &s.t. \quad \sum\limits^N_{i=1}\alpha_i y_i = 0 \\ &\qquad \quad 0 \le \alpha_i \le C, i=1,2,...,N \end{aligned}\]可以看到,\(\xi\)不见了,它比线性可分支持向量机多了一个\(\alpha_i \le C\) 不过需要注意的是\(b^*\)的公式也变了
非线性支持向量机(核技巧)
可以看到下图中的数据,可以用一个椭圆形的分类边界将数据分类, 也就是将原来的\(x\)映射到二维\(z=x^2\)可以将数据很好的分割

根据上面的思路,我们将\(x\)映射到更高维,\(\phi(x)\), 则\(wx+b\)就变成了\(w\phi(x)+b\)
核函数
我们定义核函数\(K(x,z)=\phi(x)\bullet\phi(z)\)
我们看个例子,假设核函数\(K(x,z)=(x\bullet z)^2\),\(x,z\)均是2维的, 那么\(\phi(x)=((x^{(1)})^2, \sqrt{2}x^{(1)}x^{(2)}, (x^{(2)})^2)\),可以使得核函数成立
那这个时候,我们就可以不用求\(\phi\)具体是什么,只要直接使用\(K(x,z)\)
当然核函数需要满足一定条件才能这么干,常用的核函数有, 多项式核函数:\(K(x,z)=(x\bullet z+1)^p\) 高斯径向基函数:\(K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})\)
在SVM中使用
决策函数为,
\[f(x) = sign(\sum\limits^N_{i=1} \alpha_i^* y_i (x\bullet x_i)+b^*)\]我们映射到高维,
\[f(x) = sign(\sum\limits^N_{i=1} \alpha_i^* y_i (\phi(x)\bullet \phi(x_i))+b^*)\]转化成核函数,
\[f(x) = sign(\sum\limits^N_{i=1} \alpha_i^* y_i K(x, x_i)+b^*)\]SVM对比Logistic Regression
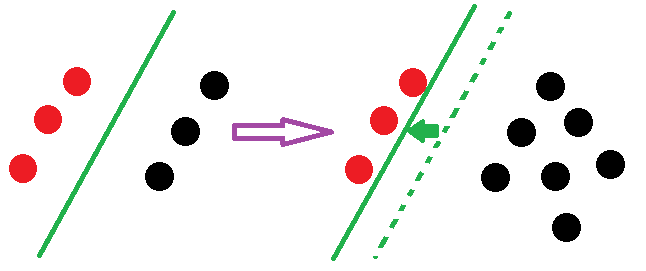
1、SVM只关心一部分点,而LR关心所有的点
SVM增加点后的状况
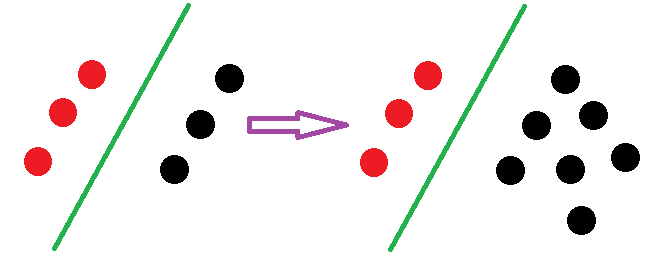
LR增加点后的状况